Tipos de funciones

Una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, rango o ámbito).

De manera más simple: Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera corresponde un único valor de la segunda.

La función se puede ilustrar mediante un diagrama usando flechas para indicar la forma en que se asocian los elementos de los dos conjuntos.

Básicamente, hay tres formas para expresar una función: mediante una tabla de valores (como el ejemplo anterior), mediante una expresión algebraica o, como veremos luego, mediante una gráfica.

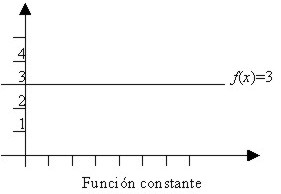
Función constante

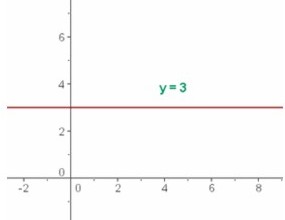
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.

Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. al.

Función lineal

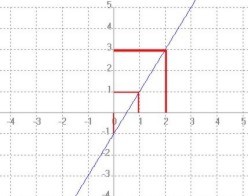
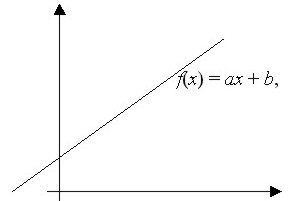
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.

Ejemplo:

F(x) = 2x - 1

 m = 2  (0, -1). 

Ejemplo:

Graficar la siguiente función:

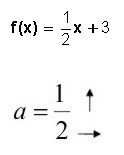
La ordenada al origen (3) me indica que me debo parar sobre el eje y en el 3.

.

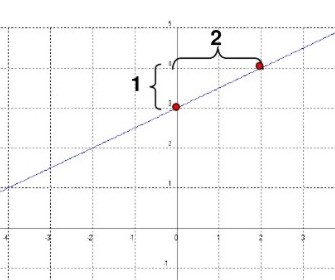
Ejemplo:

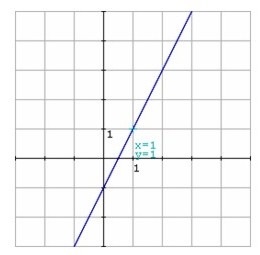
  f(x) = 2x – 1

Solución

                          Si  x = 0, f (0) = 2(0) – 1 = - 1

                          Si  x = 2,  f (2) = 2(2) – 1 = 3

Así, los puntos obtenidos  son (0, -1) y (2, 3), por los cuales se traza la gráfica  correspondiente.

Función polinómica

Función cuadrática

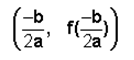
Ejemplo:

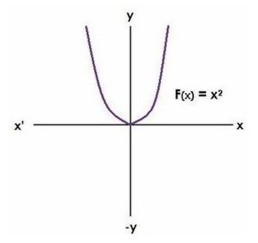F(x) = x2  representa una parábola que abre hacia arriba con vértice en (0,0).

Función racional

Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio, se tiene:

a  f(x) = xr, 

Las funciones f(x) = x4/3 y  h(x) = 5x3/2 

a): f (x) = 4x.

  f (x) = x + 2.
f (x) = x/2 - 1
 f (x) = (x - 1)2

1) El volumen de un gas está determinado por la presión (a temperatura constante), esta relación viene dada por la ley de Boyle-Mariotte:

3) Dada la función  f(x) = 5x2 + 2

 x = 2.

  x = 2

 F (2) = 5(2)2  + 2

 F (2) = 22

 x = 2, 

  f (2) = 22.

Ejemplo:

  El precio de arrendar un auto es de 15 dólares más 0,20 de dólar por kilómetro recorrido.

• a) Hallar la fórmula que expresa el costo del arriendo en función del número de los kilómetros recorridos.
• b) ¿Cuánto hay que pagar si se han recorrido 50 kilómetros?

c) Si han cobrado 53 dólares ¿cuántos kilómetros se han recorrido?

Veamos:

a) Si llamamos x al número de kms recorridos, la fórmula de la función es f (x) = 15 + 0,2x.

b) x = 50  

 F (50) = 15 + 0,2 • 50 = 25

c) f (x) = 53 

15 + 0,2x = 53
 x = 190

Ejemplos: